【研究成果のポイント】
・空間離散(※1)モデルをその基本的な性質を変えないまま空間連続(※2)モデルに変換(置換)する方法および適当な重み関数(※3)との積分付きの積分方程式に近似する方法を開発しました。
・ハエの脳の発生で分化を制御するDelta-Notch(※4)の相互作用に対する生物実験から,実際の生命現象における連続化に必要な重み関数の形状を明らかにしました。
・空間離散モデルに連続モデルの解析手法や,数理モデリングの手法が適用可能となり,生物の発生現象等,さまざまな現象の理解に応用が期待できます。
金沢大学新学術創成研究機構の八杉徹雄准教授と佐藤純教授は,公立はこだて未来大学と北海道大学との共同研究グループにおいて,数学的な理論と,生物実験の結果を融合させて,細胞の大きさと形状などの離散的な情報を保存したまま数式化する数理モデリングの方法を確立することに成功しました。この方法を用いることで多細胞生物の発生などの離散構造上の現象に対して理論的な解析を進めるなど,新たな数理モデリングを行うことが期待できます。
本研究成果は,2020年9月21日(日本時間)にドイツの科学雑誌『Journal of Mathematical Biology』にオンライン掲載されました。
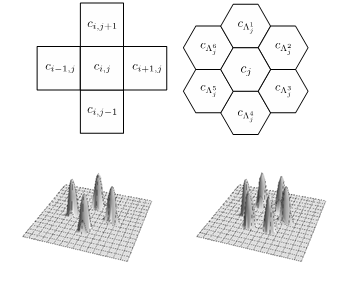
図1. 四角格子と六角格子の模式図(上図)と,対応する重み関数(下図)
発生現象の数理モデリングでは,領域を四角形や六角形の格子に分割し,各格子を一つの細胞と見なすことが多い。本研究の数理手法により,細胞や格子の大きさと形状に対応する重み関数を導出することができる。
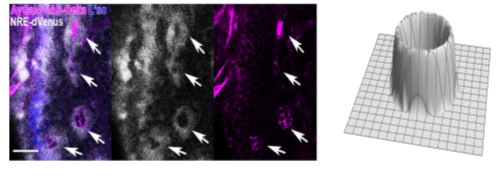
図2. 発生中のハエの脳を用いた実験結果(左)を基に提案される円環型の重み関数(右)
発生中のハエの脳では,Deltaを発現する細胞(紫)を取り囲むように円環型のNotchシグナルの活性(白)が観察された。
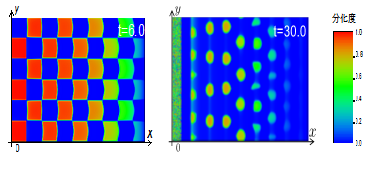
図3. ハエの脳に見られる「分化の波」の伝播現象(※5)に対する数理モデルの数値計算結果
左図は四角格子の重み関数,右は円環型の重み関数を用いた。この数値計算では,連続モデルの数値計算をしているにも関わらず,離散的な「分化の波」の伝播現象を再現した。
※1 離散
自分の周りを切り取る区間を小さくしていくと自分以外含まれなくなる集合(数直線上の整数)。生命現象を数理的に解析する際には,組織中の細胞は空間的に区切られており,組織は離散的な構造を持つ細胞の集合体として扱うことが多い。
※2 連続
自身の周りを切り取る区間を小さくしても,自身以外に元がある集合(数直線)。
※3 重み関数
合成積を計算する際に,被積分関数に掛ける,位置や場所に依存する関数。
※4 Delta-Notch
多くの生物の発生現象で用いられている細胞間相互作用の一種。細胞膜貫通型タンパク質Deltaが隣の細胞のNotch受容体と結合することにより,隣の細胞ではNotchシグナルが活性化される。
※5 「分化の波」の伝播現象
細胞が何らかの特徴的な性質を獲得する過程を「分化」という。発生中のハエの脳では一方向的に,あたかも波が伝播するように一列ずつ順番に神経分化が起きる「分化の波」現象が観察される。




 PAGE TOP
PAGE TOP