Abstract:
Point set registration problems, i.e. finding corresponding points between shapes represented as point sets, are important in a variety of fields, so algorithms have been developed. Here, a new algorithm is discovered for point set registration problems. This algorithm is demonstrated to solve several typical problems remarkably faster than conventional methods and with the highest accuracy. This novel algorithm will be beneficial to a wide variety of technologies including computer graphics, computer vision, authentication etc.
[Background]
A point set registration problem is a task using two shapes, each consisting of a set of points, to estimate the relationship of individual points between the two shapes. Here, a “shape” is like a human body or face, which is similar to another body or face but exhibits morphological diversity. Taking the face as an example: the center position of the pupil of an eye varies depending on individuals but can be thought to have a correspondence with that of another person. Such a correspondence can be estimated by gradually deforming one shape to be superimposable on the other. Estimation of the correspondence of a point on one shape to a point on another is the point set registration problem. Since the number of points of one shape could be millions, estimation of correspondence is calculated by a computer. Nonetheless, up to now, even when the fastest conventional method was used, it took a lot of time for calculation for registration of ca. 100,000 points. Thus, algorithms that could find a solution far faster without affecting accuracy have been sought. Furthermore, preliminary registration before automated estimation was a prerequisite for the conventional calculation method, so algorithms that do not need preliminary registration are desirable.
[Results]
Prof. Osamu Hirose, a young scientist at Kanazawa University, has been working on this problem. In his study, a completely new approach has been taken; a point set registration problem is defined as maximization of posterior probability*1) in Bayesian statistics*2) and the smoothness of a displacement field*3) is defined as a prior probability*4). As a result, a new algorithm has been discovered that can find a solution of a typical point set registration problem even without sufficient preliminary registration. In addition, by replacing some calculations of this algorithm with approximation, point set registration problems can be solved drastically faster than conventional methods. For example, for two point sets consisting of ca. 100,000 points each (leftmost in Figure 1), application of the present method was successful in completing highly accurate registration within 2 min, while the fastest method that was publicly available took about three hours. Also, as shown in Figure 2, the proposed method successfully registered the “dragon” dataset, where both point sets were composed of 437,645 points each. The computing time was roughly 20 min. Although the present high-speed calculation uses approximations, the accuracy of registration is not reduced to a discernible extent, as demonstrated by numerical experiments.
By using the algorithm, new CG characters can be automatically created, and thereby, it can be a labor-saving technique for CG designers. Figure 3 shows an example application of the algorithm. Source shape (a) and target shape (b) were obtained from a public database and used as input of the algorithm. Shape (c) is the result of the first registration, showing that the source shape became similar to the target shape with characteristics of the source shape retained. Shape (d) is the result of the second registration, showing the source shape to be deformed closer to the target shape. The video summary of this research is available at the following website: [https://youtu.be/cET6gKAvjw0].
[Future prospects]
The importance of point set registration problems is due to their wide range of applications in the fields of computer graphics (CG) and computer vision. Personal authentication by face recognition used on smartphones can be interpreted as an application of point set registration. Further, blending the 3-dimensional shape of certain two persons, called “morphing,” can be performed through point set registration. In addition, there is a well-known study that enabled restoration of a 3-dimensional face model of the late Audrey Hepburn from a single picture, which used a technique that can be interpreted as point set registration. Therefore, since point set registrations having a wide variety of applications can now be performed at a very high speed with high accuracy, it is expected that the method established in this study will be used as a core technology in this research field.
On the other hand, the method could be further improved. Although it is remarkably faster than the conventional method, calculation speed may become a problem when the number of points in a point set reaches millions. Prof. Hirose is further developing methods to enable calculation of such a large point set registration problem within several minutes. Preliminary results show great promise for successful further developments.

Figure 1. The result of the present method applied to data referred to as “armadillo.”
The red shape is made by a non-rigid deformation of the blue shape; the two shapes are not superimposable on each other by shape rotation. The leftmost shape represents the initial placement, showing that preliminary point set registration has not been performed prior to automated registration. The optimization process is shown from left to right.

Figure 2. Application of the algorithm to the "dragon" dataset.
This animation shows the evolution of shape deformation, resulting from the application of the algorithm to the dragon dataset. As for the armadillo dataset, the red shape before optimization was created by nonlinear deformation of the blue shape. Both point sets are composed of 437,645 points each.
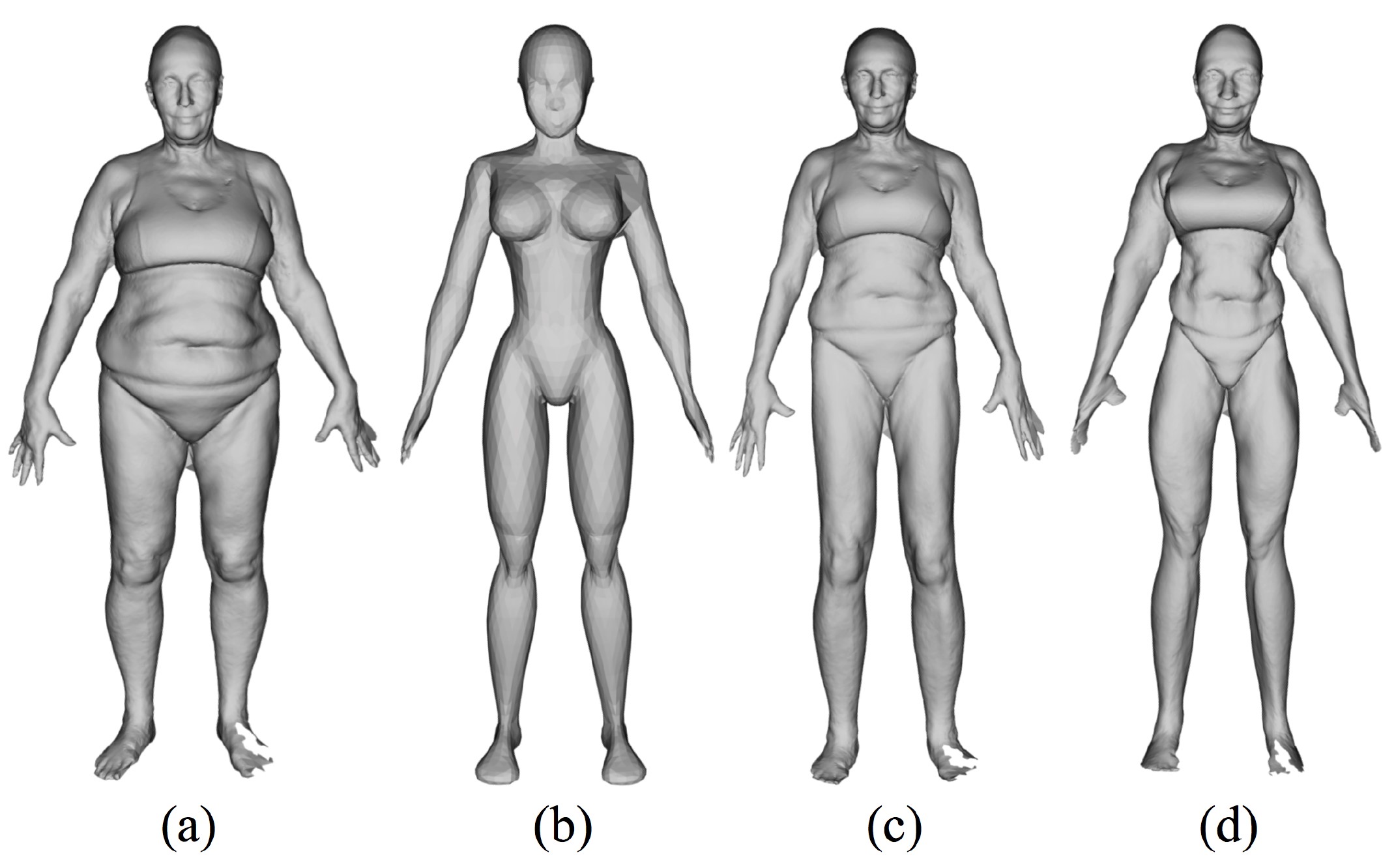
Figure 3. Example of shape transfer by applying the present method.
(a) Source shape. (b) Target shape of point set registration. (c) Shape after the first registration. (d) Shape after the second registration.
[Glossary]
*1) Maximization of posterior probability
The probability of a hypothesis being true after observing some outcomes is called the posterior probability. In Bayesian statistics, the best possible hypothesis is determined by finding the one that maximizes the posterior probability.
*2) Bayesian statistics
A category of statistics that introduces a prior probability, playing a role in prior knowledge for improving an inference from data.
*3) Smoothness of displacement field
The assumption that displacement vectors to define a shape deformation gradually become parallel as the distance between points decreases. It has been known from the early phase of this research field that this assumption remarkably improves accuracy of registration.
*4) Prior probability
A type of probabilities used in Bayesian statistics. It can be interpreted as the probability of a hypothesis being true without observations, and it plays a role in prior knowledge reinforcing an inference. In this study on point set registration problems, smoothness of displacement field is introduced as a prior probability.
Article
A Bayesian Formulation of Coherent Point Drift
Journal: IEEE Transactions on Pattern Analysis and Machine Intelligence
Authors: Osamu Hirose



 PAGE TOP
PAGE TOP